Die ersten Sätze, die ich als Kind über Computer gehört habe, waren: „Computer sind nicht schlauer als Menschen, sie können nur schneller rechnen“ und „Computer kennen nur Nullen und Einsen“. Aber wie bitte soll man damit rechnen? Und wo stecken diese Nullen und Einsen eigentlich? Lasst es uns herausfinden! Heute erklären wir in einfachen Worten das Binär-System.

Kopfrechnen
Beginnen wir mit einigen einfachen Überlegungen: Computer sind Maschinen, die Menschen erfunden haben, damit sie ihnen das Rechnen abnehmen. Das erkennt man schon am Namen „Computer“ (englisch für „Rechner“). Was heißt das überhaupt „Rechnen“? Schauen wir uns zunächst an, wie wir Menschen das machen. Angenommen wir erhalten auf einem Blatt Papier die Aufgabe „12 + 3 = ?“. Was passiert dann? Zunächst lesen wir mit unseren Augen die Zeichen. Unser Gehirn kombiniert: „Aha, das sind zwei Zahlen und dazwischen ist ein Pluszeichen. Ich soll zusammenzählen.“ Im Kopf addieren wir die zwei Zahlen und kommen auf „15“. Das schreiben wir als Ergebnis der Aufgabe auf das Blatt.
Zusammengefasst sind das die folgenden drei Schritte:
1) Erkennen der Zahlen und Zeichen
2) Addieren der Zahlen
3) Aufschreiben des Ergebnis
Das sind entsprechend auch die drei Schritte, die einer Maschine beigebracht werden müssen, damit man sie Computer nennen kann.
Computer gehen zum Lernen nicht in die Schule
Nun ist aber schon Schritt 1 für Maschinen schwierig. Sie haben keine Augen oder andere Sinnesorgane wie wir Menschen. Sie sind auch nicht in die Schule gegangen und haben gelernt dass bei einer „12“ die hintere Ziffer für die „Einer“ und die vordere Ziffer für die „Zehner“ steht. Das könnte ja auch genau andersherum sein. Der Computer muss also wissen, um welche Ziffer es sich handelt und wofür sie steht.
Dazu stellen wir uns den Computer erst mal als eine einfache schwarze Kiste vor und denken noch nicht darüber nach, was sich darin befindet. Auf eine Seite der Kiste schreiben wir „Zahl A“ und auf die gegenüberliegende Seite „Zahl B“, dazwischen ein Pluszeichen, weil „Zahl A“ und „Zahl B“ addiert werden sollen. Unten auf die Kiste schreiben wir „Ergebnis“.
Jetzt stecken wir in die beschrifteten Seiten einige Drähte. Jeder Draht stellt eine Ziffer dar. Also beschriften wir die Drähte mit „Einer“, „Zehner“, „Hunderter“, „Tausender“. Das sieht dann so aus wie auf der Abbildung.
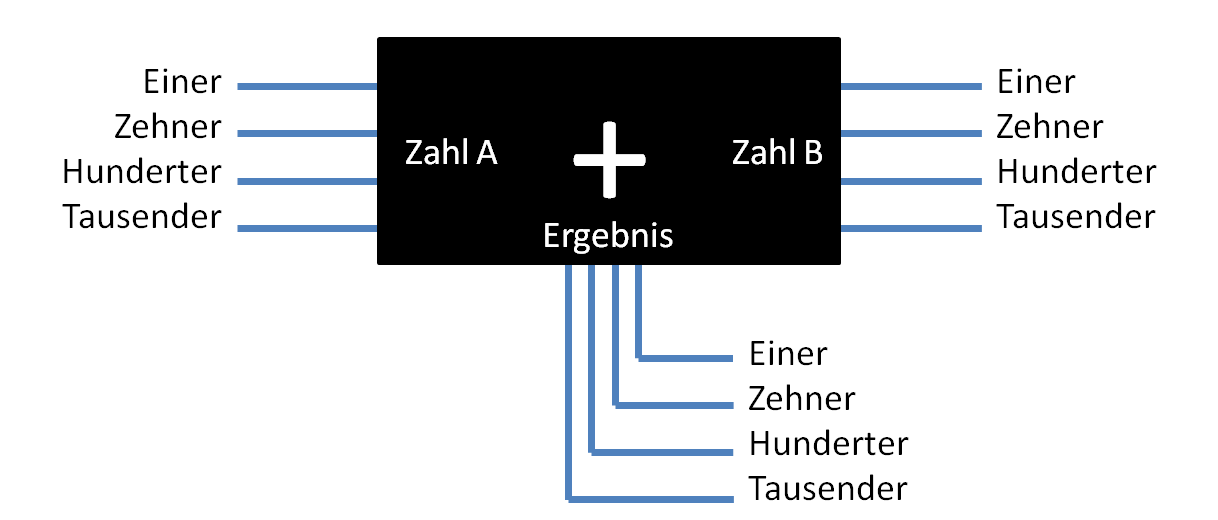
Die Idee ist: Die Drähte werden an eine Stromquelle angeschlossen. Um dem Computer mitzuteilen mit wieviel Einern, Zehnern usw. er rechnen muss, müssen wir auf den jeweiligen Draht entsprechend Strom geben. Also, wenn Zahl A eine „1“ ist, dann geben wir auf den Einer-Draht ein wenig Strom, für die „2“ ein bisschen mehr, für die „3“ noch etwas mehr und so weiter. Beispielsweise für die Zahl „13“ geben wir dann auf den Zehner-Draht ein wenig Strom und beim Einer-Draht so viel Strom wie bei einer „3“. Auf der Ergebnisseite messen wir dann einfach, bei welchen Drähten wieviel Strom herauskommt. Genial, oder?
Das Stromproblem
In der Theorie funktioniert das, aber in der Praxis ist das knifflig. Jede Ziffer kann zehn verschiedene Zahlensymbole haben. Je nachdem, ob die Ziffer eine 0, 1, 2, 3, 4, 5, 6, 7, 8 oder 9 ist, müssten wir etwas mehr oder etwas weniger Strom auf den Draht geben. Und an den Ergebnis-Drähten müssten wir ganz genau messen, wie viel Strom dort rauskommt. So genau Strom zu geben und zu messen, bekommen wir nicht zuverlässig genug hin. Richtig zuverlässig können wir eigentlich nur zwei Zustände messen: Strom an oder Strom aus. Statt der zehn Symbole müssen wir uns also auf zwei beschränken.Und damit sind wir bei den Nullen und Einsen angekommen: Wir nehmen „0“ für Strom-aus und „1“ für Strom-an.
Zehn-Symbole-System und Zwei-Symbole-System
Doch wie rechnet man jetzt nur mit Nullen und Einsen? Das ist ungewohnt, weil wir unserem Kopf das Zehn-Symbole-System (Dezimalsystem) antrainiert haben. Im Dezimalsystem bedeutet jede Ziffer „zehn hoch irgendetwas“. Nehmen wir als Beispiel die Zahl 1111. Sie setzt sich zusammen aus:
- 1 Tausender = 1000 = 10 · 10 · 10 = 103
- 1 Hunderter = 100 = 10 · 10 = 102
- 1 Zehner = 10 = 101
- 1 Einer = 1 = 100 (eine Zahl hoch 0 ist immer 1)
Wenn man jetzt statt zehn nur zwei Symbole zur Verfügung hat, dann steht jede Ziffer eben nicht für „zehn hoch irgendwas“ sondern für „zwei hoch irgendwas“. Die Ziffern 1111 bedeuten dann:
- 23 = 2 · 2 · 2 = 8 = 1 „Achter“
- 22 = 2 · 2 = 4 = 1 „Vierer“
- 21 = 2 = 1 „Zweier“
- 20 = 1 = 1 „Einer“
Man merkt hier: Wenn man nur zwei Symbole zur Verfügung hat, dann benötigt man viel mehr Ziffern zur Darstellung einer Zahl als im Dezimalsystem. Im Dezimalsystem sind wir bei der vierten Ziffer schon in den Tausendern. Im Zwei-Symbole-System sind wir da erst bei den Achtern. Die Zahl fünf zum Beispiel benötigt in Dezimalsystem nur eine Ziffer, nämlich „5“. Im Zwei-Symbole-System benötigen wir schon drei Ziffern. Beweis gefällig?
1 Vierer (1 · 22 = 4) + 0 Zweier (0 · 21 = 0) + 1 Einer (1 · 20 = 1) = 5
Die drei Ziffern „101“ (das müsst Ihr jetzt „eins-null-eins“ lesen, und eben nicht „einhundertundeins“) ergeben zusammen fünf. Das Zwei-Symbole-System funktioniert. Man nennt es auch „Dual-System“ (von lateinisch „dualis“, d.h. „zwei enthaltend“) oder Binär-System (von lateinisch „bi“, d.h. „zwei“). Eine einzelne Binär-Ziffer, die entweder eins oder null sein kann, wird kurz „Bit“ genannt (von englisch „binary digit“). Die Mathematiker kennen das System übrigens schon seit mehr als zweitausend Jahren. Es musste nicht erst für die Computer erfunden werden.
Strom und Binär-System passen zusammen
Zurück zu unserer schwarzen Kiste. Diese können wir jetzt anpassen. Wir ändern einfach die Beschriftung der Drähte. Dann sieht das so aus:
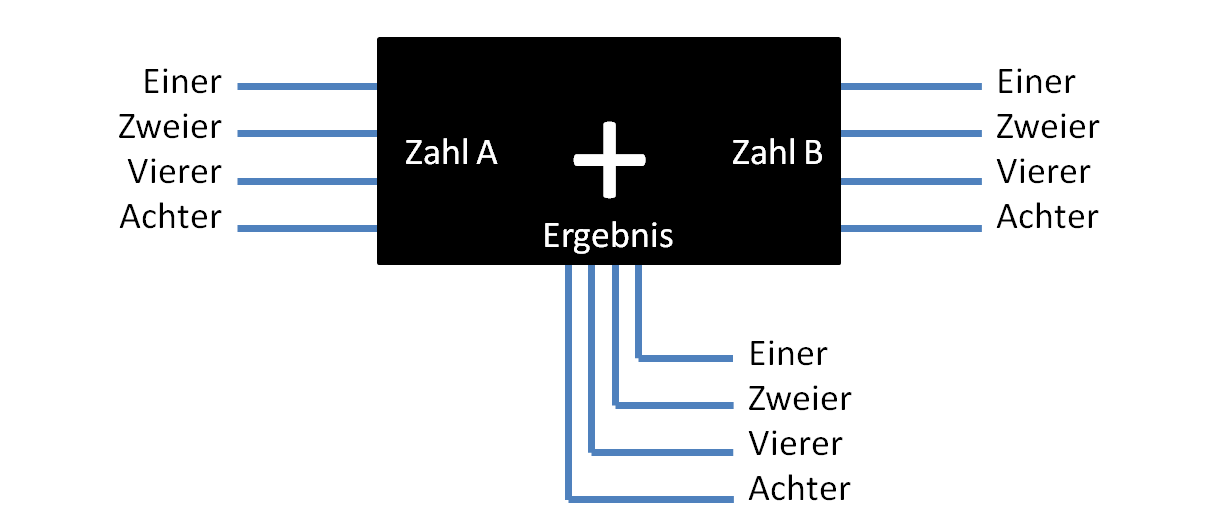
Man sieht auch hier wieder, dass wir für größere Zahlen viel mehr Drähte benötigen würden. Wir bleiben daher in unserem Beispiel bei kleinen Zahlen und geben unserer schwarzen Kiste eine einfache Aufgabe, sagen wir „5 + 2“. Zahl A ist also „5“, in Binärschreibweise „101“ (1 Vierer, 0 Zweier, 1 Einer). Zahl B ist die „2“, in Binärschreibweise „10“ (1 Zweier, 0 Einer). Jetzt geben wir auf die richtigen Drähte Strom, so wie wir es festgelegt haben. „Strom-an“ ist in der Abbildung rot dargestellt (entspricht einer Ziffer „1“). Für „Strom-aus“ bleibt die Farbe blau (entspricht Ziffer „0“).
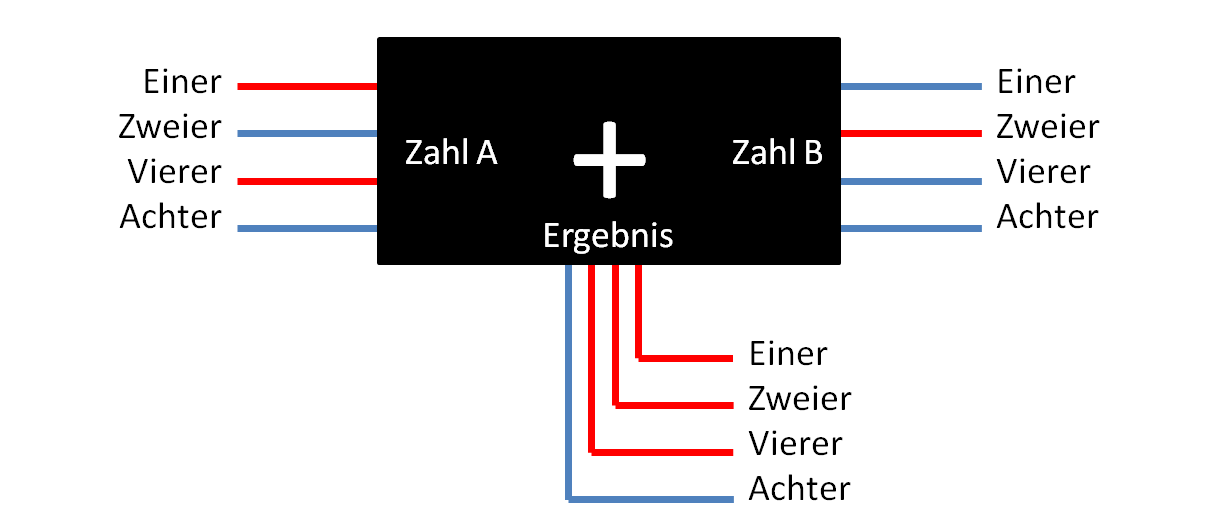
Wir sehen jetzt, dass unten auf der Ergebnisseite drei Drähte rot geworden sind: Einer, Zweier und Vierer, also ist das Ergebnis in Binärschreibweise „111“. Ein Einer, ein Zweier und ein Vierer ergibt in unserem gewohnten Dezimalsystem „7“. Die komplette Aufgabe ist demnach „5+2=7“. Die schwarze Kiste hat richtig gerechnet.
Ein erstes Zwischenfazit: Die Einsen und Nullen kommen also daher, dass man einem Computer Aufgaben nur in Form von „Strom ein, Strom aus“ geben kann und er seine Ergebnisse auch nur in „Strom ein, Strom aus“ mitteilen kann. Diese zwei Zustände werden symbolisiert durch Einsen und Nullen. Man hätte aber auch „X/Y“ oder „blau/rot“ oder irgendwelche anderen Symbole nehmen können.
Binärzahlen zusammenzählen
Mit unserem Schwarze-Kiste-Ansatz konnten wir zeigen wie die Aufgabe herein und das Ergebnis herauskommt. Was innerhalb der Kiste passiert, haben wir uns noch nicht angesehen. Das ist aber notwendig, um zu verstehen, wie das Zusammenzählen der zwei Zahlen tatsächlich funktioniert. Irgendetwas im Innern der Kiste muss ja so schlau sein, um zu wissen, welche Drähte im Ergebnis unter Strom gesetzt werden müssen.
Wir beschränken uns im Folgenden auf das Zusammenzählen von zwei Zahlen mit nur einer Ziffer. Wie rechnen wir das im Dezimalsystem? Wir zählen die Einer zusammen und wenn die Summe zehn oder mehr ergibt, dann schreiben wir einen Übertrag auf die Zehner. Der Übertrag ergibt dann unter dem Strich im Ergebnis eine weitere Ziffer:
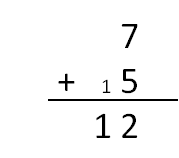
Im Binärsystem funktioniert das genauso: Wir zählen die Einer zusammen und wenn die Summe zwei ergibt schreiben wir einen Übertrag. Da beide Zahlen nur 0 oder 1 sein können, gibt es generell nur vier mögliche Ergebnisse: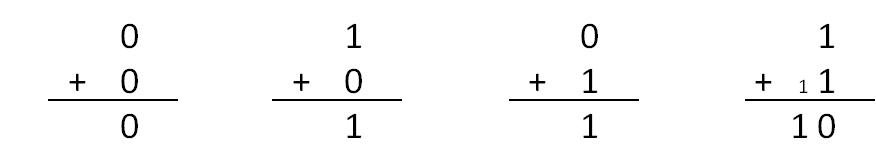
Wir können hier zwei Dinge erkennen:
- Die Ziffer für die Zweier unter dem Strich ist nur dann „1“, wenn Zahl A und Zahl B beide den Wert „1“ haben. In allen anderen Fällen gibt es keinen Übertrag.
- Die Ziffer für die Einer unter dem Strich ist nur dann „1“, wenn Zahl A und B unterschiedliche Werte haben. Also entweder Zahl A oder Zahl B muss „1“ sein. Sind dagegen beide gleich, dann steht unter dem Strich bei den Einern eine „0“.
Stromschaltungen zum Rechnen
Die zwei oben genannten Bedingungen müssen wir jetzt durch eine geschickte Stromschaltung innerhalb der schwarzen Kiste umsetzen. Beginnen wir mit der Bedingung für den Zweier: In der Kiste bringen wir eine Stromquelle an (auf der Abbildung der rote Punkt) und verbinden diese mit dem Zweier-Draht. Hier ist der Strom immer an. Zusätzlich bauen wir zwei Schalter ein. Einen Schalter verbinden wir mit dem Draht von Zahl A, den anderen mit dem Draht von Zahl B. Wenn durch den jeweiligen Draht Strom fließt, schließt sich der Schalter. Fließt durch den Draht kein Strom, bleibt der Schalter offen. Nur wenn beide Schalter geschlossen sind, kommt der Strom unten an. Damit hätten wir die Schaltung für den Zweier.
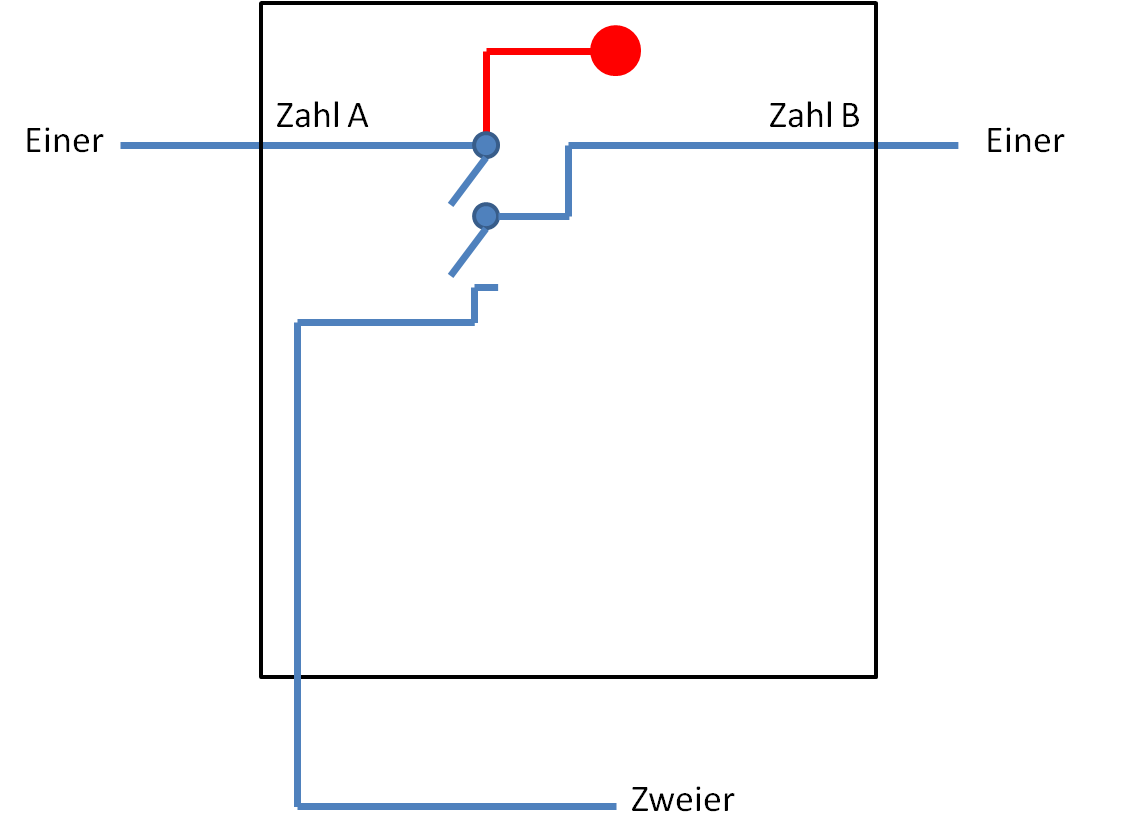
Jetzt benötigen wir noch eine Schaltung für die Einer im Ergebnis. Wir schließen auch diesen an die Stromquelle in der Kiste an, jedoch mit zwei parallelen Drähten. In beiden Drähten gibt es je einen Schalter, der mit dem Draht von Zahl A bzw. mit dem Draht von Zahl B gesteuert wird. Allerdings funktionieren die Schalter gegensätzlich. Wenn Zahl A Strom liefert, schließt sich der Schalter A1 und Schalter A2 öffnet sich. Wenn Zahl B Strom liefert, schließt sich der Schalter B1, dafür öffnet sich der Schalter B2. Das ganze führt dazu, dass im linken oder im rechten Draht nur dann Strom von oben nach unten fließen kann, wenn entweder Zahl A oder Zahl B Strom liefern, aber nicht beide gleichzeitig. Damit haben wir auch die Schaltung für den Einer fertig.
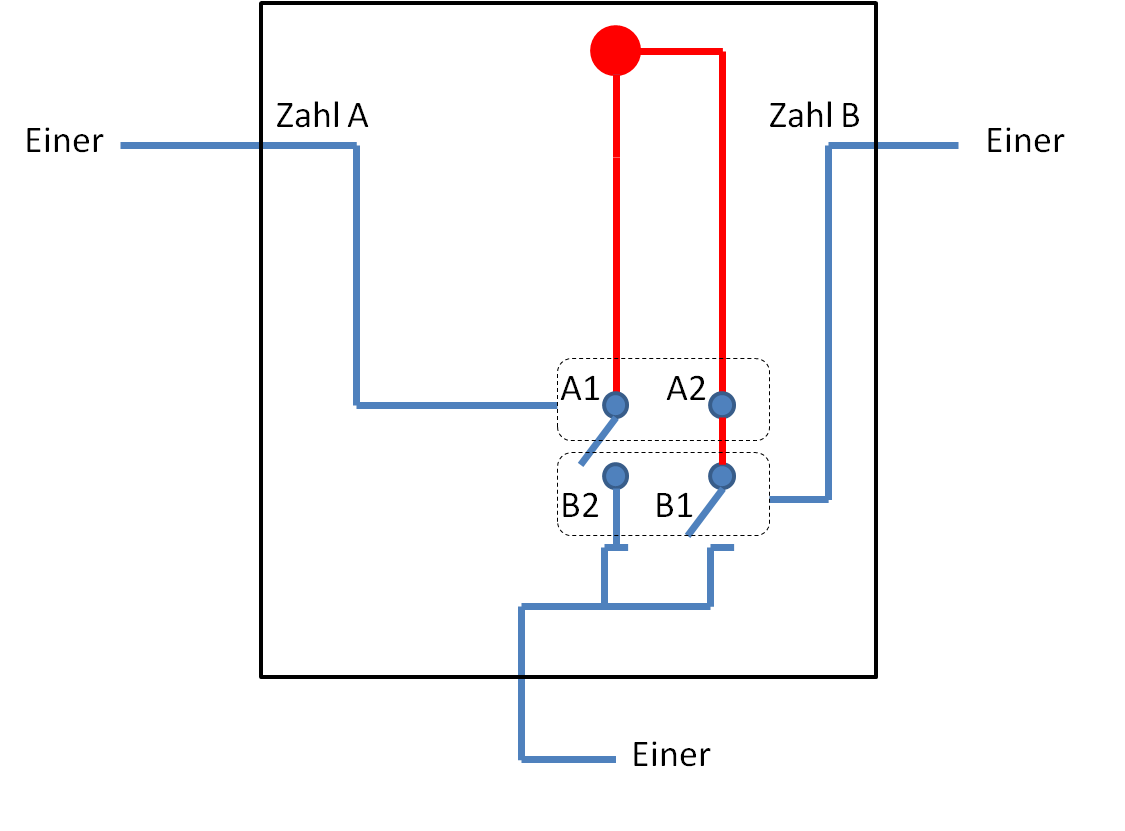
Das Innere der Kiste
Jetzt müssen wir die beiden Schaltungen nur noch zusammen in der Kiste anbringen. Die beiden Drähte von Zahl A bzw. Zahl B teilen sich dafür auf. In der Abbildung sehen wir auch bereits: Wenn die Drähte von Zahl A und Zahl B beide nicht unter Strom stehen, dann kommt auch bei den Ergebnisdrähten unten kein Strom an. Das entspricht der Rechnung 0 + 0 = 0.
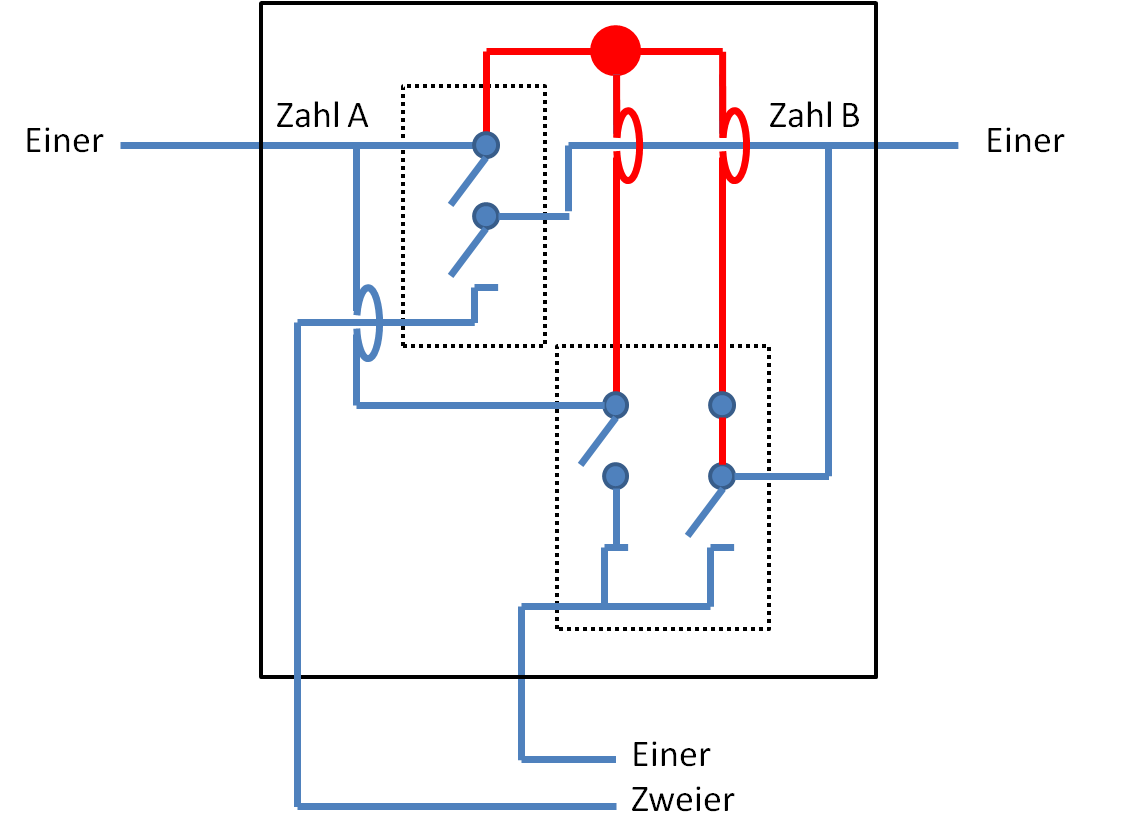
Jetzt geben wir Strom auf Zahl A. Die Schalter öffnen bzw. schließen sich wie oben beschrieben. Im Ergebnis liefert nun der Einer-Draht Strom. Der Zweier-Draht nicht. Die Rechnung 1 + 0 = 1 ist korrekt.
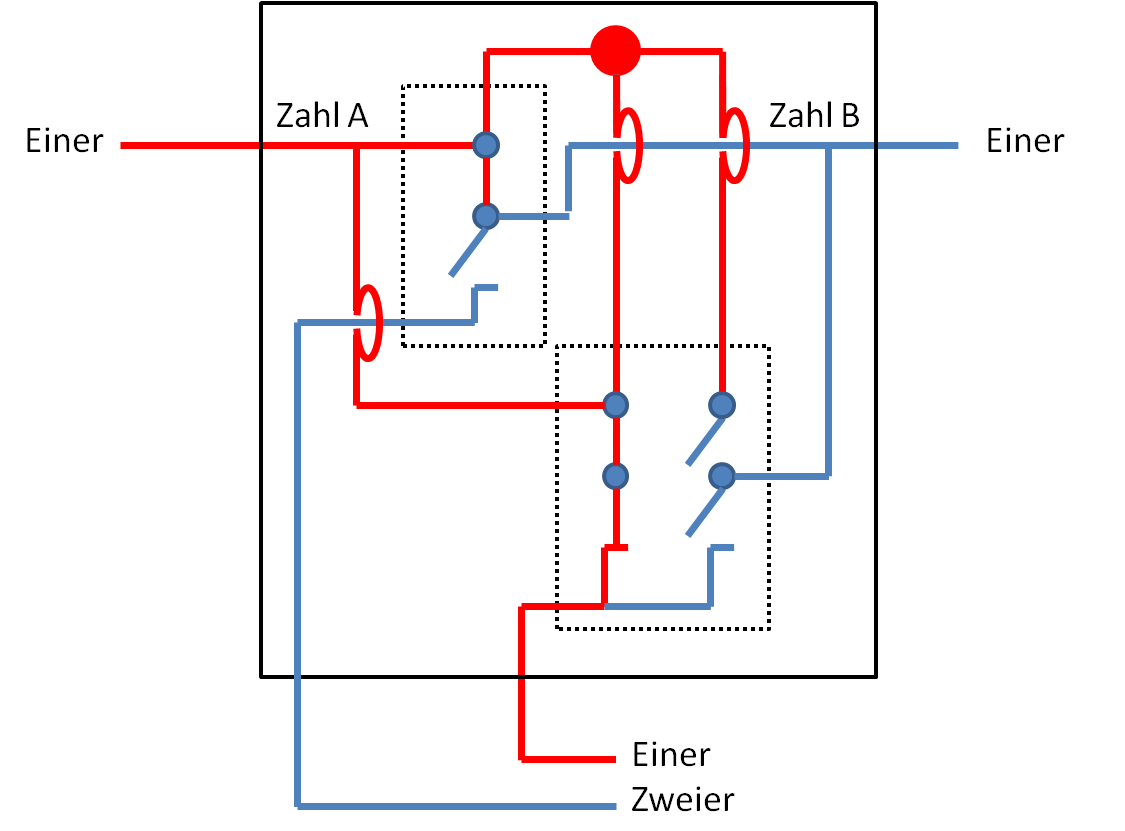
Nun drehen wir das um, geben auf Zahl B Strom anstatt auf Zahl A. Die Schalter ändern sich, aber im Ergebnis bleibt alles gleich, denn auch 0 + 1 = 1.
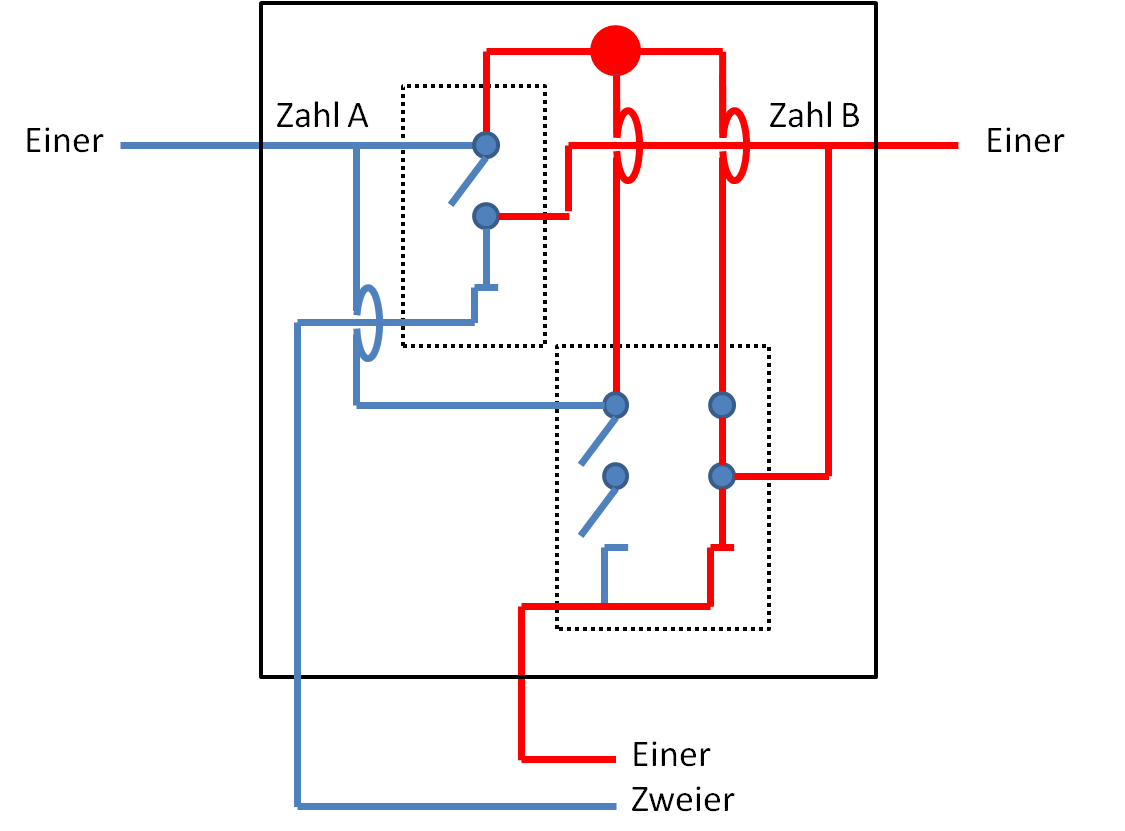
Fehlt noch der letzte Fall: Wir geben bei beiden Zahlen Strom. Im Zweier-Draht sind nun beide Schalter geschlossen, daher kommt im Ergebnis Strom an. Auf dem Einer-Draht jedoch nicht. Das entspricht der Rechnung 1 + 1 = 10. Das Ergebnis stimmt also auch hier.
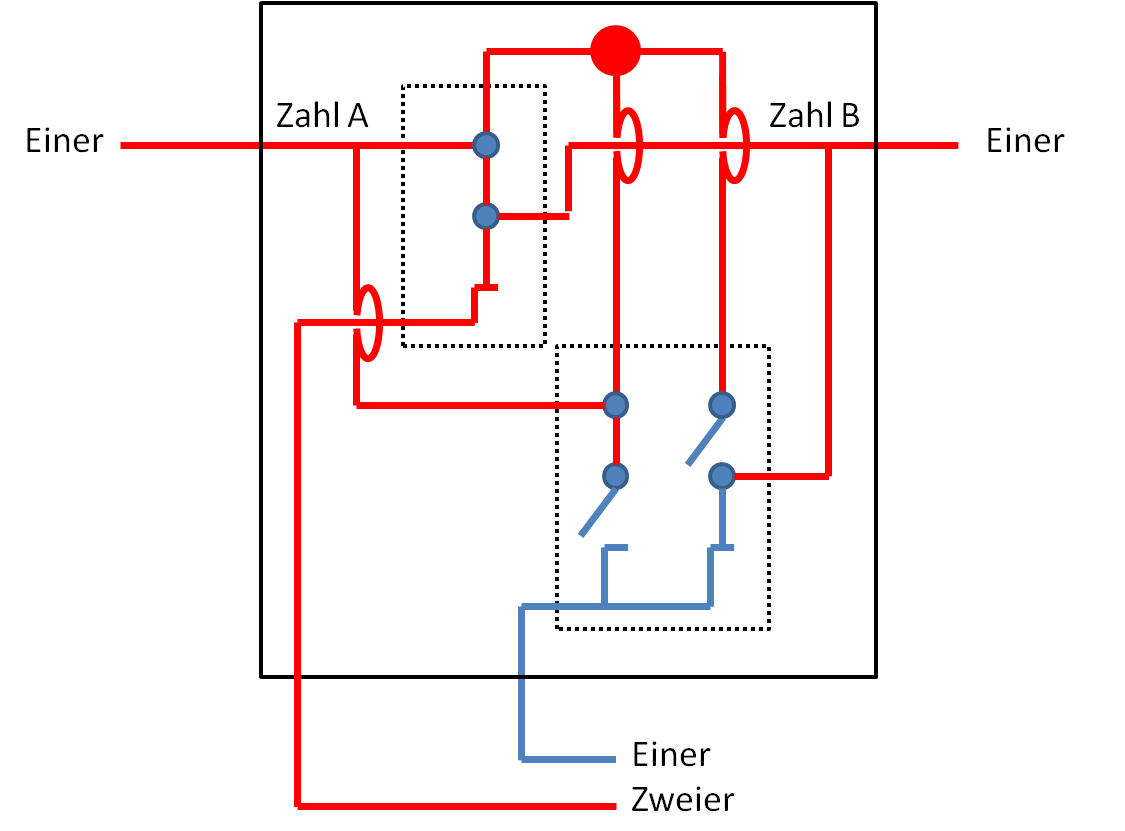
Bausteine zum Rechnen
Die oben beschriebene Schaltlogik zum Zusammenzählen von zwei Zahlen mit je einer Ziffer nennt man „Halbaddierer“. Muss man zu den zwei Ziffern (Zahl A und Zahl B) noch einen Übertrag addieren, benötigt man einen zusätzlichen Strom-Eingang. Man spricht dann von einem „Volladdierer“ (3 Eingänge). Wenn man die Volladdierer dann hintereinanderschaltet, so dass der Übertrag aus einem Volladdierer in den nächsten Volladdierer wandert, kann man prinzipiell beliebig große Zahlen addieren. Die Abbildung zeigt das Addieren mit vier Ziffern beginnend bei den Einern ganz rechts in einem Halbaddierer. Wenn es bei einer Ziffer einen Übertrag gibt, wird dieser an den Volladdierer links daneben weitergegeben.
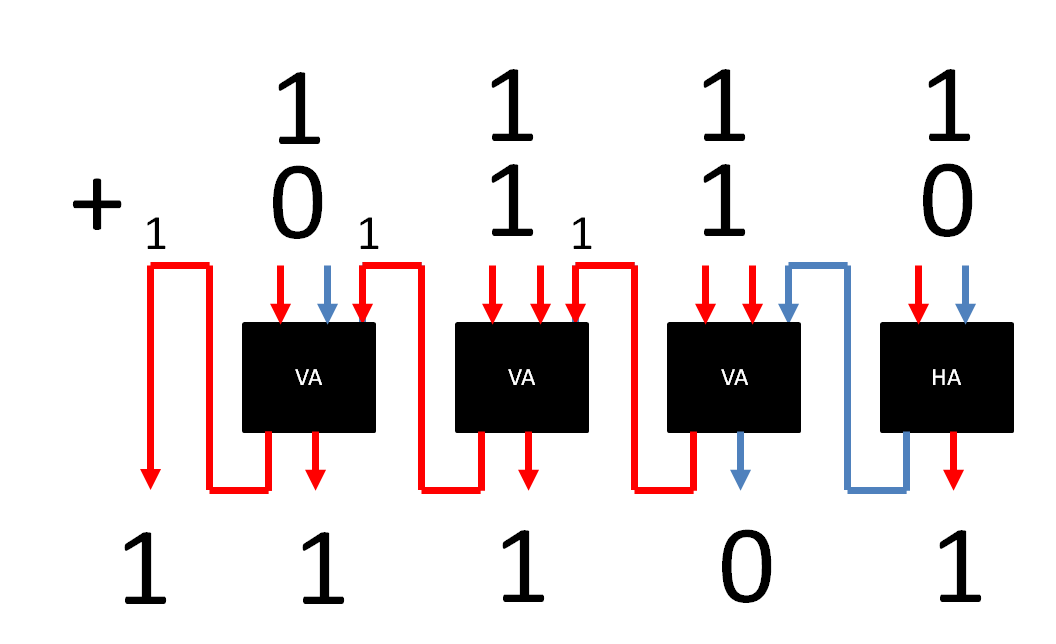
Natürlich gibt es nicht nur das Addieren. Man kann mit Binärzahlen auch subtrahieren, multiplizieren und dividieren. Dafür hat man ebenfalls geeignete Bausteine.
Computerchips
Wir haben oben gesehen wie man mit zwei Zuständen (Strom an / Strom aus) rechnen kann. Die notwendigen Bausteine werden in sehr großer Anzahl und sehr kleiner Form in winzigen Computerchips verbaut. Je kürzer und dünner die Drähte sind, durch die der Strom fließt, desto schneller wird der Computer. Mittlerweile ist man in einem Bereich, wo praktisch jedes Atom zählt und wir nähern uns der ultimativen Grenze von einer Atomdicke (etwa ein Millimeter geteilt durch zehn Millionen).
Dann ist theoretisch Schluss mit dem klassischen Computerchipbau. Doch es gibt bereits Ideen für eine ganz andere Art Computer, der auf noch kleinerer Ebene als Atome – der Quantenebene – arbeitet. Diese sogenannten Quantencomputer sollen im Laufe des 21. Jahrhunderts noch einmal einen gigantischen Geschwindigkeitssprung bringen. Doch obwohl das dann nicht mehr auf dem Prinzip Strom an / Strom aus basiert, sehen die Konzepte weiterhin das Rechnen auf Basis des Binär-Systems vor. Aus Bits werden dann Qubits („Quanten-Bits“), aber alles andere bleibt uns erhalten. Wie genau so ein Quantencomputer funktionieren könnte, ist allerdings eine andere Internetgeschichte.
Für heute lassen wir es gut sein mit den Nullen und Einsen. Dieser Beitrag hat nun exakt 2048 Wörter. Im Binär-System ist das die Zahl 100000000000. Wer mag, kann das gerne nachrechnen. 😉
 Wer Zahlen und Computer mag, dem wird besonders Internetgeschichten Teil #7 – Einfach erklärt: Verschlüsselung gefallen. Oder beginnt doch einfach ganz von vorne bei Internetgeschichten Teil #1 – Was Restaurants und Computernetze gemeinsam haben.
Wer Zahlen und Computer mag, dem wird besonders Internetgeschichten Teil #7 – Einfach erklärt: Verschlüsselung gefallen. Oder beginnt doch einfach ganz von vorne bei Internetgeschichten Teil #1 – Was Restaurants und Computernetze gemeinsam haben.
Für Fragen, Kritik oder Anregungen schickt mir gerne weiterhin Nachrichten, gebt mir Rückmeldung über die Kommentarfunktion unten oder nutzt die Facebook-Seite zum Blog. Und falls es Euch gefallen hat, lasst ein „Daumen-hoch“ da. 🙂