500 Millionen(!) ausgespähte Passwörter fand das Bundeskriminalamt im Jahr 2017 auf einem Server an einem einzigen Tag. Das waren damals schockierende Nachrichten und für viele ein Ende der Sorglosigkeit im Internet. Doch die Frage, wie man geheime Dinge effektiv vor Kriminellen schützt, ist immernoch aktuell. Programme wie WhatsApp oder Zoom bieten praktische Möglichkeiten zur Kommunikation, aber bleibt geheim, was man sich dort gegenseitig erzählt? Das wird immer wieder angezweifelt und diskutiert. Damit Ihr mitdiskutieren könnt, widmen wir uns in diesem Teil der Internetgeschichten der Waffe gegen Spione: Verschlüsselung. Wir nähern uns mit einfachen Worten und Beispielen einem Fachgebiet, das sonst den Mathematikern vorbehalten ist.

Würdet Ihr intime Geheimnisse lieber in eine Postkarte schreiben oder in einen Brief? Wohl eher Letzteres, denn Ihr wollt nicht, dass jeder mitlesen kann. Im Internet gilt das Gleiche: Jeder Webseiten-Aufruf, jede E-Mail, jede WhatsApp-Nachricht – wie Ihr aus den letzten Beiträgen wisst, läuft alles über die Computer fremder Leute. Und wenn Ihr nicht wollt, dass diese alles mitlesen können, müsst Ihr einige Dinge beachten.
Spionage in der Schulbank
Kommen wir nochmal zurück auf Romeo und Julia aus Teil #6 der Internetgeschichten. Die beiden Schüler sitzen im Klassenzimmer in der ersten Reihe. Um sich miteinander verständigen zu können, schicken sie sich kleine Zettel hin und her. Die Mitschüler zwischen Romeo und Julia reichen den Zettel dabei jeweils an ihren Nachbarn weiter. Zur Erinnerung: Genau wie die Schüler bilden Computer im Internet eine Kette. Jede Nachricht wird von einem Computer an den nächsten weitergeben bis sie ihr Ziel erreicht.
Wir wissen jetzt, wie die beiden verhindern können, dass ein Man-in-the-middle Nachrichten fälscht. Dazu setzen sie ein Zeichen auf die Nachricht, zum Beispiel durch einen seltenen Stempel, den nur die beiden besitzen. Das funktioniert prima, aber es hat immernoch einen Haken: Die Mitschüler können zwar die Nachricht nicht mehr verändern, aber jeder kann problemlos mitlesen. Was können Romeo und Julia also tun?
Verschlüsselung mit echten Schlüsseln
Die Antwort ist „Verschlüsselung“. Aber was ist das genau? Gehen wir das einmal durch: Im Wort „Verschlüsselung“ steckt das Wort „Schlüssel“ drin. Romeo und Julia nehmen sich ein kleines abschließbares Kästchen, zu dem beide einen Schlüssel besitzen. Romeo legt eine Nachricht in das Kästchen, schließt mit seinem Schlüssel ab und reicht es seinem Sitznachbarn. Da dieser keinen Schlüssel hat, kommt er nicht an den Inhalt der Nachricht heran. Der Zugang dazu ist für ihn „verschlossen“, oder eben „verschlüsselt“. Und so wandert das Kästchen bis zu Julia. Sie kann es mit ihrem Schlüssel aufschließen (wir nennen es „Entschlüsseln“) und die Nachricht lesen. Dann legt sie ihre Nachricht wieder hinein, schließt ab und reicht das Kästchen zurück. Eine solche Verschlüsselung vom Verfasser bis zum vorgesehenen Leser einer Nachricht – also vom einen Ende der Sitzreihe zum anderen – nennen wir Ende-zu-Ende-Verschlüsselung.
Verschlüsselung durch Geheimsprache
Die Methode mit dem Kästchen ist zweifellos schon ein bisschen sicherer. Aber echte, anfassbare Schlösser können unter Einsatz von roher Gewalt geöffnet werden. Wenn es einer der Mitschüler ernst meint, zerlegt er einfach das Kästchen in seine Einzelteile. Romeo und Julia müssen sich eine bessere Methode ausdenken.
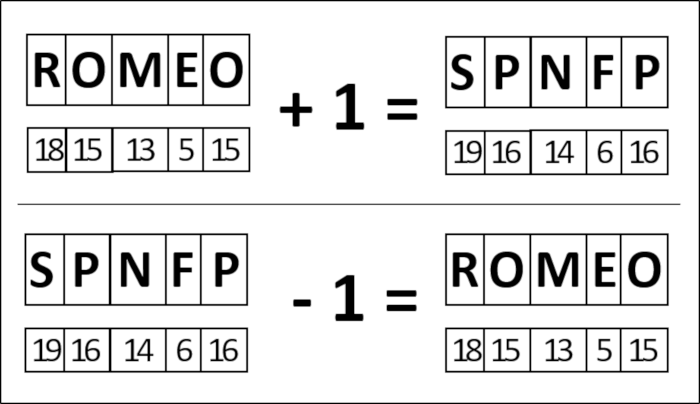
Sie einigen sich daher auf eine Geheimsprache. Dafür stellen sie sich das gesamte Alphabet in einer Reihe vor. A steht ganz links und Z ganz rechts. Dann vereinbaren sie: Wir verschieben in unseren Nachrichten jeden Buchstaben um eine Stelle nach rechts. Aus „A“ wird „B“, aus „B“ wird „C“ und ganz hinten aus „Z“ wird wieder „A“. So wird zum Beispiel aus ROMEO das unleserliche Wort SPNFP. Und derjenige, der die Nachricht erhält, muss umgekehrt jeden Buchstaben um eine Stelle nach links verschieben. Damit wird die Nachricht wieder lesbar. Aus SPNFP wird wieder ROMEO.
Das erinnert immer noch ein wenig an einen echten Türschlüssel. Den dreht man zum Abschließen in die eine Richtung und zum Aufschließen in die umgekehrte Richtung. Romeo und Julia schieben die Buchstaben zum Verschlüsseln nach rechts und zum Entschlüsseln ebenfalls in die umgekehrte Richtung nach links. Daher sprechen wir auch bei solchen Geheimschrift-Tricks von einem „Schlüssel“. Der Schlüssel in die eine Richtung angewendet, erzeugt Buchstabensalat (korrekt „Geheimtext“ genannt), den Schlüssel umgekehrt angewendet erzeugt wieder lesbaren Text (den sogenannten „Klartext“).
Buchstabensalat und brutale Gewalt
Romeo und Julia tauschen nun ihre Nachrichten in Geheimschrift aus. Die Mitschüler sehen nur Buchstabensalat, mit dem sie nichts anfangen können, weil sie den Geheimschrift-Schlüssel nicht haben. Der Schlüssel, den sich Romeo und Julia ausgedacht haben, ist aber leider immer noch nicht besonders sicher. Durch ein wenig Ausprobieren und Knobeln könnte ein Mitschüler den Geheimschrift-Schlüssel erraten und dann doch mitlesen.
Ausprobieren ist generell etwas, das auch Computer sehr gut können. Sie nehmen einfach der Reihe nach alle bekannten Geheimschrift-Schlüssel und schauen, ob etwas Sinnvolles dabei herauskommt. Computer sind schnell und langweilen sich nicht, selbst wenn sie zehntausend verschiedene Schlüssel erfolglos ausprobiert haben. Ein Computer benötigt dafür nicht viel Cleverness sondern einfach nur Kraft und Ausdauer ähnlich wie ein Mensch, der mit der Brechstange ein Vorhängeschloss aufbricht. Daher nennen Informatiker das dumpfe Durchprobieren von Schlüsseln auch „brute force“ (Englisch für „brutale Gewalt“).
Um Computer gegen Brute Force zu schützen, haben sich Mathematiker daher kompliziertere Geheimschrift-Methoden ausgedacht, bei denen seeehr viele Schlüssel infrage kommen. Um diese Schlüssel alle auszuprobieren, würde selbst der schnellste Computer der Welt viele Jahre benötigen.
Verschlüsselung ist Mathematik
Warum jetzt eigentlich Mathematiker? Weil man den Geheimtext immer berechnen kann. Im Beispiel oben verschieben Romeo und Julia die Buchstaben im Alphabet um eine Stelle. Wenn wir alle Buchstaben durchnummerieren („A = 1“, „B = 2“ usw.), muss man „plus 1“ zum Verschlüsseln und „minus 1“ zum Entschlüsseln rechnen. Die Rechnung ist demnach:
Nummer Originalbuchstabe + 1 = Nummer Zielbuchstabe
Nummer Zielbuchstabe – 1 = Nummer Originalbuchstabe
Am Beispiel des Worts ROMEO sieht das so aus:
Hier gibt es genau eine Umkehraufgabe und alles basiert darauf, dass die Zahl „1“ geheim bleibt. Man könnte natürlich auch jede andere Zahl (Geheimzahl) nehmen. Die Geheimzahl ist dann sozusagen der Schlüssel zum Lösen der Aufgabe. Wenn vorwärts und rückwärts die gleiche Zahl verwendet wird, es also nur einen Schlüssel gibt, dann nennen wir das eine „symmetrische“ Verschlüsselung.
Computer nehmen dafür wirklich, wirklich große Zahlen. Bei aktuellen Verschlüsselungsmethoden haben sie 39 oder 78 Stellen (oder sogar noch mehr). Das macht es dann anderen Computern so schwer, die richtige Zahl durch Ausprobieren zu erraten. Stellt Euch vor, Ihr müsstet ein Zahlenschloss mit 78 Stellen durch Raten öffnen! Die Mathematiker Vincent Rijmen und Joan Daemen entwickelten im Jahr 2000 unter der Bezeichnung „Rijndael“ eine solche symmetrische Verschlüsselung, die bis heute als sicher gilt. Sie ist allerdings nicht unter ihrem ursprünglichen Namen bekannt geworden, sondern unter der Bezeichnung Advanced Encryption Standard (AES) (englisch für „fortschrittlicher Verschlüsselungsstandard“).
Schlüsselpaare
Romeo und Julia sollten sich demnach auf eine Geheimzahl einigen, die man weniger leicht erraten kann. Klingt vernünftig, aber wir ignorieren dabei ein Problem. Wir haben nämlich vorausgesetzt, dass Romeo und Julia sich vorher im Geheimen abstimmen können. Was aber, wenn sie die Gelegenheit gar nicht haben? Sie müssten sich über die Mitschülerreihe erst einmal auf ihren Geheimschrift-Schlüssel verständigen. Aber dann hätten ja alle Mitschüler den Geheimschrift-Schlüssel und er wäre dann eben nicht mehr geheim. Es wäre sinnlos, die Nachrichten damit zu verschlüsseln.
Hierfür haben sich die Mathematiker Whitfield Diffie, Martin Hellman und Ralph Merkle in den 1970er Jahren eine geniale Idee einfallen lassen: In den Beispielen oben war der Schlüssel zum Verschlüsseln und Entschlüsseln immer der gleiche. Er musste nur jeweils vorwärts bzw. rückwärts angewendet werden. Die Mathematiker erfanden jetzt Schlüsselpaare, bei denen das nicht ging. Wie das Romeo und Julia hilft, sehen wir gleich. Schauen wir uns zunächst an, wie das Ausrechnen funktioniert.
Asymmetrische Verschlüsselung
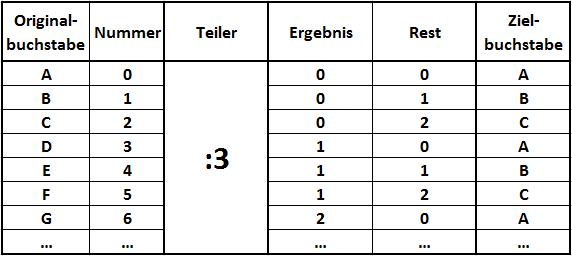
Wir können zum Beispiel festlegen, dass wir alles durch die Zahl 3 teilen und dann den „Rest“ als Nummer des Zielbuchstaben nehmen. Dazu nummerieren wir die Buchstaben nochmal neu durch. Diesmal bekommt das A die „0“, B die „1“, usw. Schauen wir uns an, was bei der Berechnung des Zielbuchstaben herauskommt:
Als „Rest“ ergeben sich nur die Werte „0“, „1“ und „2“. Das sind die Nummern der Buchstaben „A“, „B“ und „C“. Also werden auch nur diese drei Buchstaben als Zielbuchstabe verwendet. Wenn wir jetzt umgekehrt rechnen wollen, ist das nicht mehr so einfach. Hat man zum Beispiel den Zielbuchstaben „A“, dann kommen mehrere Originalbuchstaben in Frage: „A“, „D“, „G“, und so weiter. Um also zurück auf den Originalbuchstaben zu kommen, reicht es nicht aus, den Teiler (hier die Zahl „3“) zu kennen. Das heißt, man muss die Zahl „3“ auch gar nicht geheim halten, sie kann öffentlich bekannt sein.
Um rückwärts zu rechnen, benötigt man eine zusätzliche Information, nämlich die Zahl aus der Spalte „Ergebnis“. Dann kann man folgendes rechnen:
Ergebnisspalte · Teiler + Nummer Zielbuchstabe = Nummer Originalbuchstabe
Hat man den Zielbuchstaben „A“ (also Rest „0“), die öffentliche bekannte Zahl „3“ und z.B. die Zahl „2“ aus der Ergebnisspalte, kann ich rechnen:
2 · 3 + 0 = 6 (demnach ist der Originalbuchstabe das „G“)
Die öffentlich bekannte Zahl (Teiler) und die geheime Zahl (Ergebnisspalte) sind also die zwei Schlüssel zum Lösen der Aufgabe. Damit hätten wir dann die genannten Schlüsselpaare. Sie bestehen aus:
- einem öffentlichen Schlüssel, mit dem man verschlüsseln kann, aber nicht rückwärts entschlüsseln
- einen geheimen zweiten Schlüssel, mit dem man wieder entschlüsseln kann
Im Gegensatz zu den symmetrischen Verschlüsselungen, bei denen es nur einen Schlüssel gibt, nennen wir die Verschlüsselung mit einem öffentlichen und einem geheimen Schlüssel „asymmetrisch“.
Die häufigste Art der asymmetrischen Verschlüsselung im Internet
Unser Beispiel im vorangegangenen Abschnitt sollte das Prinzip der asymmetrischen Verschlüsselung verdeutlichen. In der Praxis wäre es nicht geeignet, denn die Ergebnisspalte hat viele verschiedene Werte, die man zur Entschlüsselung wissen müsste. Die drei Mathematiker Ronald Rivest, Adi Shamir und Leonard Adleman haben sich Ende der 1970er Jahe eine Rechnung einfallen lassen, bei welcher es immer nur eine Geheimzahl benötigt. Aus den Anfangsbuchstaben der Nachnamen leitet sich der Name „RSA-Verschlüsselung“ ab, auf der noch immer ein Großteil der Verschlüsselung im Internet basiert. Ich stelle die Rechnung im folgenden Abschnitt kurz vor und habe es möglichst einfach gehalten, setze aber dennoch ein kleines Warnzeichen davor. Wer sich gerne mit Mathe beschäftigt, kann es lesen. Alle anderen dürfen das jetzt gerne überspringen und beim erhobenen Daumen fortfahren.
![]()
Die Modulo-Funktion (Restwert-Funktion) ist prima geeignet zur Verschlüsselung, da man sie nicht rückwärts rechnen kann und bei großen Zahlen auch das Ausprobieren nicht mehr in Frage kommt. Mit bestimmten Zahlen-Trippeln kann man dann folgende Rechnungen machen. Die Zahlen 1 und 2 sind öffentliche Schlüssel. Mit diesen wird verschlüsselt.
Originalbuchstabe(Zahl 1) mod (Zahl 2) = Geheimbuchstabe
Für die Umkehraufgabe wird die geheime Zahl 3 benötigt. Sie ist der private Schlüssel. Mit ihr kann wieder entschlüsselt werden.
Geheimbuchstabe(Zahl 3) mod (Zahl 2) = Originalbuchstabe
Ein Beispiel für die öffentlich bekannten Zahlen wären 23 und 143. Die zugehörige Geheimzahl ist die 47. Wenn wir den Buchstaben G (Stelle 7) verschlüsseln wollen, kommen wir auf folgende Rechnung:
723 mod 143 = 2 (also der Buchstabe B)
Zum Entschlüsseln benötigt man die Geheimzahl. Dann kann man rückwärts rechnen:
247 mod 143 = 7
![]()
Mit Schlüsselpaaren Geheimnisse austauschen
Wie hilft das nun Romeo und Julia? Nehmen wir nochmal den Vergleich mit einem Kästchen. Zu dem Kästchen gibt es dann entsprechend:
- einen Schlüssel, mit dem man nur abschließen kann
- einen zweiten Schlüssel, mit dem aufschließen kann
Wenn Julia möchte, dass Romeo ihr eine Nachricht schickt, dann reicht sie das Kästchen inklusive des Schlüssels zum Abschließen durch die Reihe. Jeder Mitschüler darf diesen Schlüssel haben, Julia kann das egal sein. Daher nennt man diesen Schlüssel „Julias öffentlicher Schlüssel“ (englisch „public key“). Romeo legt seine Nachricht nun in das Kästchen und schließt mit dem öffentlichen Schlüssel ab. Dann reicht er es zurück. Keiner der Mitschüler hat den Schlüssel zum Aufschließen, also bleibt die Nachricht geheim. Nur Julia kann das Kästchen mit dem zweiten Schlüssel aufschließen. Diesen nennt man daher auch „Julias privater Schlüssel“ (englisch „private key“).
Damit Julia auch eine Nachricht an Romeo schicken kann, benötigt auch Romeo ein eigenes Kästchen, einen öffentlichen und einen privaten Schlüssel. Jeder der beiden hat also ein eigenes Kästchen mit eigenem Schlüsselpaar. Obwohl der Übertragungsweg öffentlich ist, kann also dennoch eine geheime Nachricht übertragen werden. Das war eine der genialsten Erfindungen des 20. Jahrhunderts und die Grundlage für freie Kommunikation im Internet.
Verschlüsselung von Webseiten
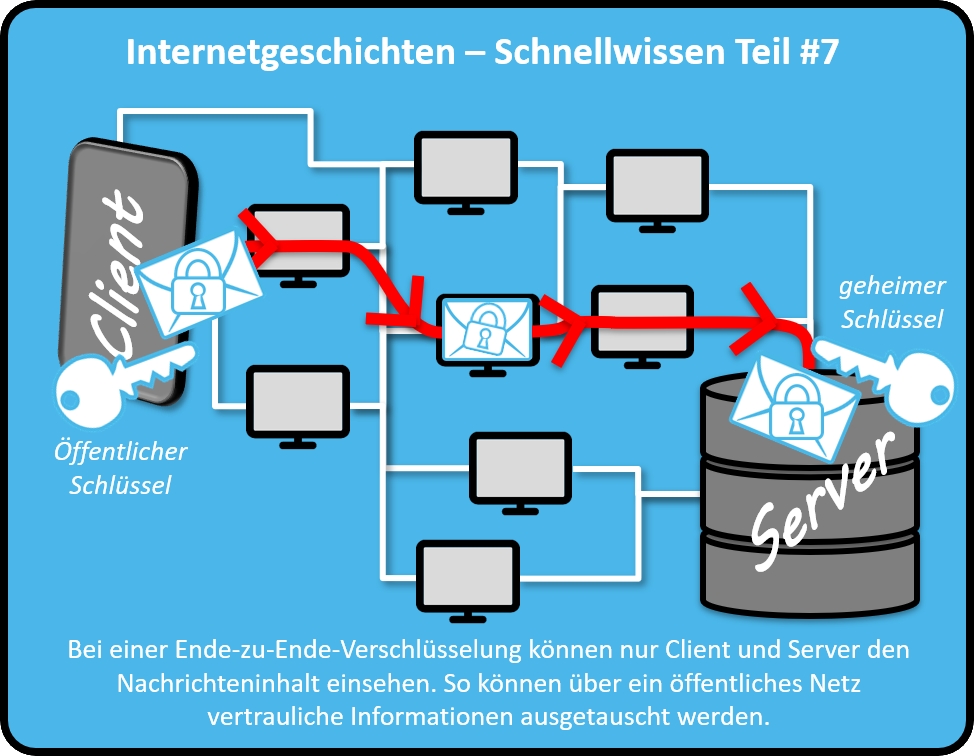
Ich hatte schon im Beitrag zum Man-in-the-middle auf das Vorhängeschloss hingewiesen, das die gängigen Internet-Browser links oben neben der Adresszeile anzeigen. Dieses signalisiert auch, dass die Verbindung zwischen Client (also Eurem Computer) und dem Server, der eine Webseite bereitstellt, verschlüsselt ist.

Nochmal in Kürze: Der Inhaber einer Domäne lässt sich den Besitz durch eine vertrauenswürdige Zertifizierungsstelle bestätigen und erhält dafür ein Zertifikat. Dieses hinterlegt er auf seinem Server. Vor einem Webseitenaufruf frägt Euer Client den Server erst einmal nach seinem Zertifikat. Damit kann sich der Client sicher sein, dass er beim richtigen Server gelandet ist. Im Zertifikat steht zusätzlich aber auch der öffentliche Schlüssel des Servers.
Mit diesem öffentlichen Schlüssel des Servers kann der Client eine erste verschlüsselte Übertragung starten (in den meisten Fällen durch die oben vorgestellte RSA-Methode). In dieser teilt der Client dem Server einen neuen symmetrischen Schlüssel (meist über die Rijndael bzw. AES-Methode) mit. Anschließend wird nur der symmetrische Schlüssel verwendet, da das schneller geht. Das ist sozusagen die Begrüßungsprozedur zwischen Client und Server. Sie wird auch als Handshake (englisch für Händeschütteln) bezeichnet. Nach dem Handshake werden dann die eigentlichen Nachrichten verschlüsselt ausgetauscht.
Zukunftssichere Verschlüsselung
Bei der Verschlüsselung in Computernetzen haben wir grundsätzlich aber noch ein Dilemma. Wir wollen natürlich immer schnellere Computer bauen und freuen uns über jeden Fortschritt. Das birgt für heutige Verschlüsselungsverfahren jedoch auch eine Gefahr. Bei der oben erklärten Brute-Force-Methode hatten wir gesagt, dass der schnellste Computer heute viele Jahre benötigen würde um eine gute Verschlüsselung zu knacken. Aber was ist wenn Computer in einigen Jahren hundertmal so schnell sind wie heute? Es werden bereits heute regelmäßig Verschlüsselungsverfahren als nicht mehr sicher eingestuft und aus dem Verkehr gezogen, weil heutige Computer einfach viel schneller sind als die vor zehn Jahren.
Es gibt berechtigte Bedenken, dass sich zum Beispiel Geheimdienste heute viele verschlüsselte Nachrichten für die Zukunft speichern und mit dem Computer der Zukunft dann alle entschlüsseln können. Aufgrund dieser Überlegungen sind die modernsten Verschlüsselungsmethoden zukunftssicher ausgelegt. Man nennt das „Perfect Forward Secrecy“ (englisch für die perfekte, zukunftsorientierte Geheimhaltung). Bei diesen Verfahren setzt man darauf, dass Client und Server nur mit einem kurzlebigen nicht-reproduzierbaren Wegwerfschlüssel verschlüsseln. Die Methoden zum Berechnen eines solchen Schlüssels werden als „ephemeral“ (englisch für „flüchtig“) bezeichnet. Diese Schlüssel sind vereinfacht gesagt so kurzlebig, dass man ihn in der Zukunft eben gar nicht mehr zur Verfügung hat, um ihn zu knacken.
Verschlüsselt ist nicht anonym
Zum Schluss sollten wir noch etwas Wichtiges klarstellen. Im Internet kann man durch Verschlüsselung nur verhindern, dass jemand die Nachrichten mitliest. Das ist schon einmal viel wert, aber man darf nicht den Fehler machen und das mit „Anonymität“ verwechseln.
Romeo und Julia haben durch ihre Geheimschrift eine Methode gefunden, damit die Mitschüler ihre Nachrichten nicht lesen können. Sind sie damit anonym geworden? Nein. Alle haben mitbekommen, dass Romeo und Julia Nachrichten miteinander austauschen. Ein Mitschüler könnte daraus seine Schlüsse ziehen, laut loskichern und rufen „Romeo liebt Julia, Romeo liebt Julia!“
Wenn Ihr nicht wollt, dass jemand weiß, mit wem Euer Computer im Internet Nachrichten austauscht, reicht die übliche Verschlüsselung nicht aus. Man kann immer noch nachvollziehen, mit wem Ihr chattet, welche Webseiten Ihr aufruft und wem Ihr E-Mails schreibt. Anonym im Internet unterwegs zu sein, benötigt ganz andere Überlegungen als die, die wir oben gemacht haben. Das behandeln wir aber dann in einer anderen Internetgeschichte, wenn wir uns in Richtung des sogenannten „Darknet“ bewegen.
 Habt Ihr noch Fragen zur Verschlüsselung oder wollt etwas ergänzen? War der Beitrag hilfreich? Schickt mir eine Nachricht, gebt mir Rückmeldung über die Kommentarfunktion unten oder nutzt die Facebook-Seite zum Blog. Und falls es Euch gefallen hat, lasst ein „Daumen-hoch“ da. 🙂
Habt Ihr noch Fragen zur Verschlüsselung oder wollt etwas ergänzen? War der Beitrag hilfreich? Schickt mir eine Nachricht, gebt mir Rückmeldung über die Kommentarfunktion unten oder nutzt die Facebook-Seite zum Blog. Und falls es Euch gefallen hat, lasst ein „Daumen-hoch“ da. 🙂